Supernan1994's Personal Blog
深入理解WMD算法
0. 背景
2018年Q4,我承接了公司的一个Key Result:重构机器人平台的后端架构,实现单机QPS能力提升10倍中的问答机器人重构。季度末复盘时,我们在完成QPS提升9.3倍、TP99下降至原来的1/7的同时,支撑算法部门达成机器人效果提升11%的指标。在问答重构的系统设计与实现过程中我们积累了一些值得参考的经验,因此选择一些有代表性的分享出来。本文主要介绍WMD算法的原理和在吾来的应用。
在深入了解算法之前,我们先简单了解一下『吾来机器人平台』的问答机器人的业务流程,帮助我们更好的理解WMD在业务中的使用场景。
问答机器人的数据来源是领域知识库。知识库中包含多个知识点,这些知识点由机器或人工聚类而来。每个知识点包含多个语义相同的相似问题,这些相似问题由机器和人工泛化而来。并且这些相似问题可以以同样的答案回复。下图是中关村海淀园『码上办』项目的知识库中的一个知识点。

当用户向机器人提出问题时,问答机器人会在知识库中找到最相似的相似问题,把相似问题对应的知识点的答案回复给用户。
下图是问答机器人的架构:
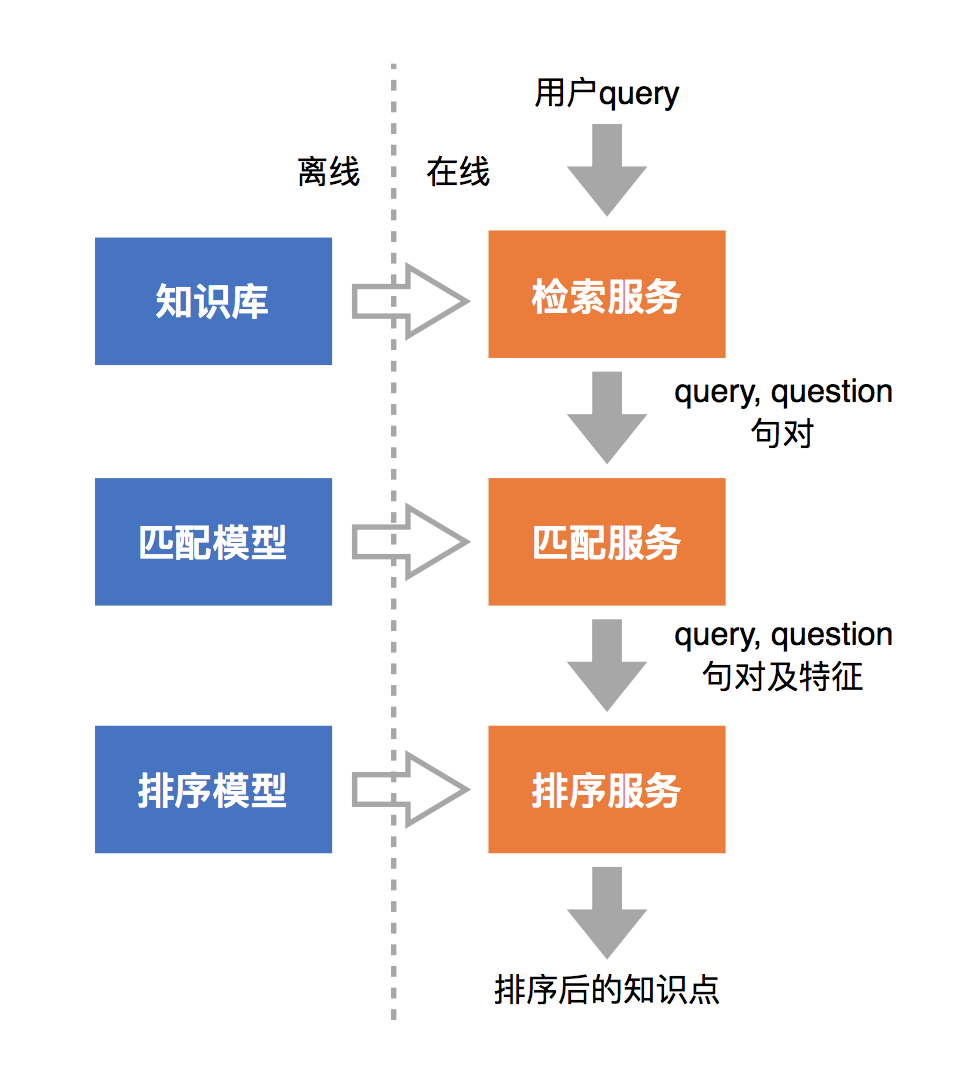
- 检索(Retrieval)
- 将每个相似问作为一个可被检索的文档
- 输出为若干个(query, question)句对
- 每个相似问题都对应一个知识点
- 匹配(Matching)
- 计算(query, question)的语义相似度特征
- 无监督特征
- 有监督特征
- 排序(Ranking)
- 知识库内的相似问,构造句对训练数据,训练有监督的模型
- 判断(query, question)的分数,选择分数最高的问题对应的知识点作为机器人回复
今天我们讨论的WMD是匹配过程中其中一个无监督的语义相似度特征。我们用WMD计算句对的文本相似度,并将它作为排序模型的一个输入,来影响问答机器人最终的回复结果。
1. 概述
WMD(Word Mover’s Distance)1是2015年提出的一种衡量文本相似度的方法。它具有以下几个优点:
- 效果出色:充分利用了word2vec的领域迁移能力
- 无监督:不依赖标注数据,没有冷启动问题
- 模型简单:仅需要词向量的结果作为输入,没有任何超参数
- 可解释性:将问题转化成线性规划,有全局最优解
- 灵活性:可以人为干预词的重要性
当然它也有一些缺点:
- 词袋模型,没有保留语序信息
- 不能很好的处理词向量的OOV(Out of vocabulary)问题
- 处理否定词能力偏差
- 处理领域同义词互斥词的能力偏差
- 时间复杂度较高:\(O(p^{3}\log{}p)\)(其中,p代表两篇文本分词去重后词表的大小)
2. WMD核心算法
2.1 形象描述
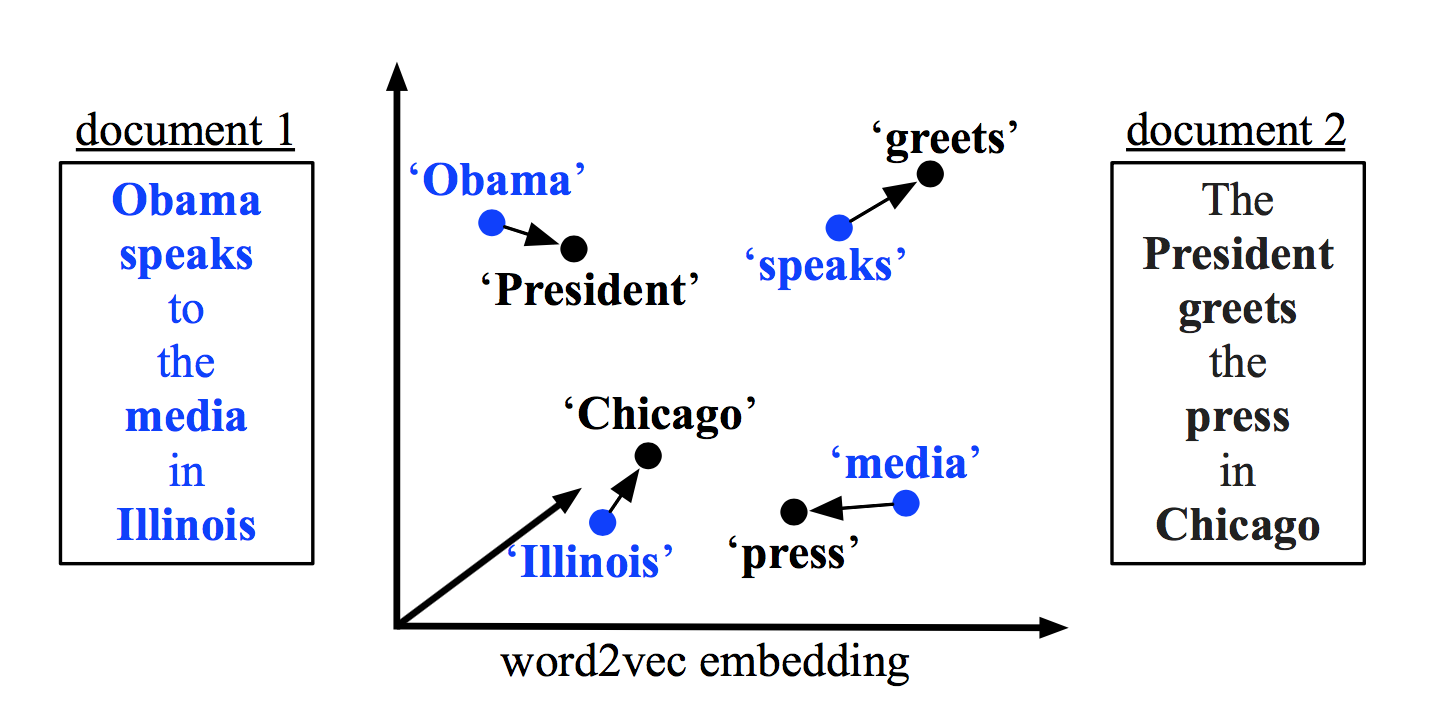
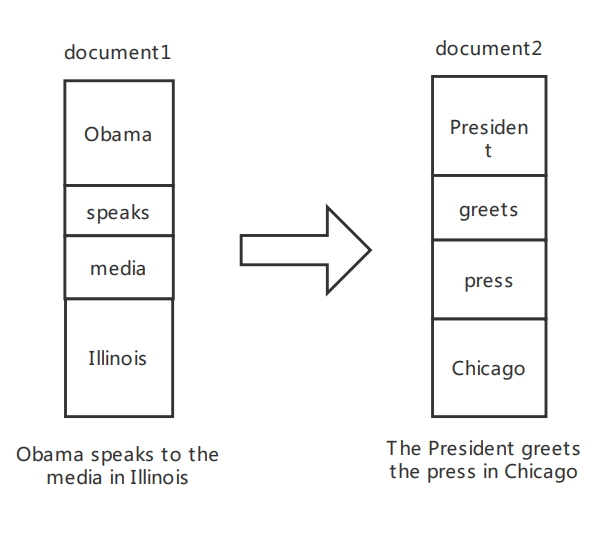
WMD的核心思想非常简单,就是我们在文章开头看到的这张图。我们可以把它看成一个运输问题:计算将仓库1的货物移动到仓库2的最小费用。在NLP的场景中,我们把2条文本当做2个大小相同的仓库,词就是仓库中的货物,那么目标就是将文本1中所有词移动到文本2中的代价最小化。
在利用WMD计算两条文本的相似度时,会进行以下步骤:
- 利用word2vec将词编码成词向量
- 去掉停用词
- 计算出每个词在文本中所占权重,一般用词频来表示
- 对于每个词,找到另一条文本中的词,确定移动多少到这个词上。如果两个词语义比较相近,可以全部移动或移动多一些。如果语义差异较大,可以少移动或者不移动。用词向量距离与移动的多少相乘就是两个词的转移代价
- 保证全局的转移代价加和是最小的
- 文本1的词需要全部移出,文本2的词需要全部移入
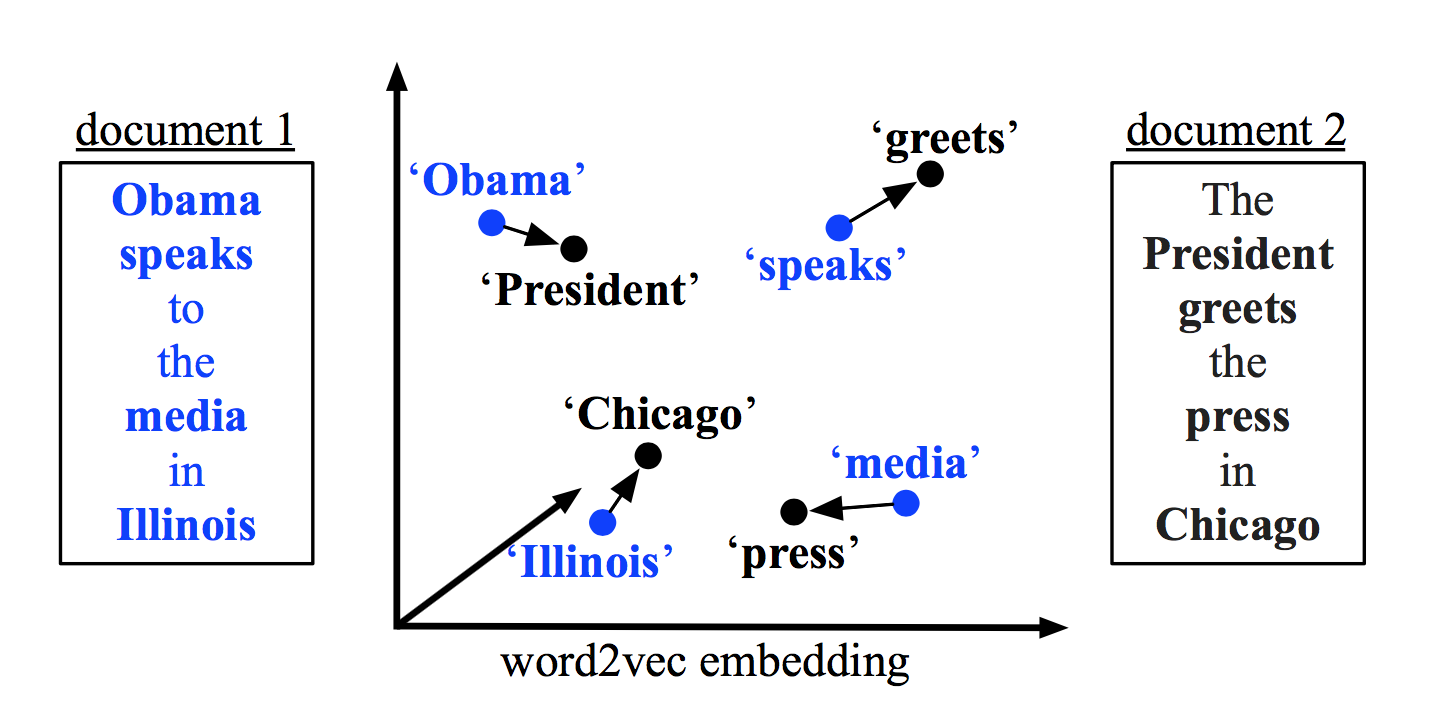
论文中给出了两个例子:
- 第一个例子是分别计算\(D_{1}\)和\(D_{2}\)与\(D_{0}\)的距离,比较哪条文本与\(D_{0}\)相似度更高。\(D_{1}\)有四个词,对于每一个词,都能找到在\(D_{0}\)中与之最相近的一个词,并计算出转移代价。与我们直观的理解相符,\(D_{1}\)与\(D_{0}\)的距离比\(D_{2}\)与\(D_{0}\)的距离更近,相似度更高。
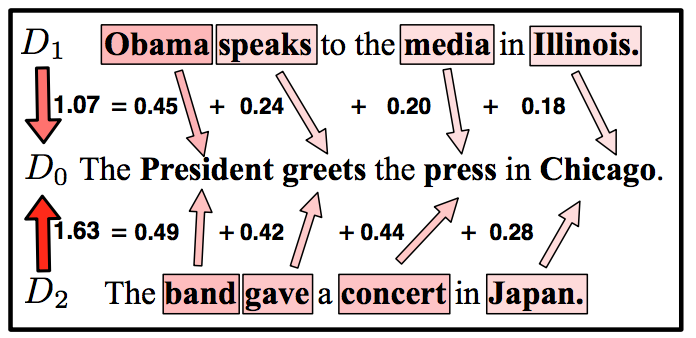
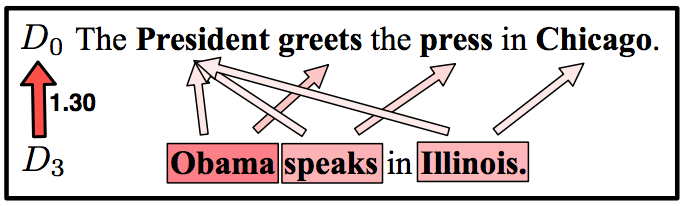
- 在第二个例子中,两条文本的词数并不一致,\(D_{0}\)中每个词的词频是\(\frac{1}{4}\),而\(D_{3}\)中每个词的词频是\(\frac{1}{3}\),因此\(D_{3}\)的每个词将对应到\(D_{0}\)多个词上。
2.2 数学描述
WMD算法用以上的思路将文本语义相似度的问题转换成了一个线性规划问题。用数学语言形式化的描述WMD所解决的问题:
首先,假设有一个训练好的词向量矩阵\(\textbf{X}\in\mathbb{R}^{d \times n}\),一共有\(n\)个词。第\(i\)列\(\textbf{x}_{i}\in\mathcal{R}^{d}\)代表第\(i\)个词的\(d\)维词向量。词\(i\)与词\(j\)欧氏距离为
\[c(i,j)=\Vert\textbf{x}_{i}-\textbf{x}_{j}\Vert_{2}\]一条文本可以用稀疏向量\(\textbf{d} \in \mathcal{R}^{n}\)作为词袋表示,如果在文本中词\(i\)出现了\(c_{i}\)次,\(\textbf{d}\)的第i位就是第i个词的词频\(d_{i}\)
\[d_{i}=\frac{c_{i}}{\sum_{j=1}^{n}c_{j}}\]我们令\(\textbf{d}\)和\(\textbf{d}'\)分别代表要计算的两条文本的词袋表示,\(\textbf{d}\)中的每个词\(i\)都可以全部或部分地转移到\(\textbf{d}'\)。因此,定义一个稀疏的转移矩阵\(\textbf{T}\in\mathcal{R}^{n \times n}\),\(\textbf{T}_{ij}\)代表了有多少从\(\textbf{d}\)中的词\(i\)转移到\(\textbf{d}'\)中的词\(j\),\(\textbf{T}_{ij}\ge 0\)。进一步地得出从\(\textbf{d}\)到\(\textbf{d}'\)转移代价的和为\(\sum_{i,j}\textbf{T}_{ij}c(i,j)\)。
最终我们将最小化转移代价的和转化为线性规划问题:
s.t.
\[\sum_{j=1}^n\textbf{T}_{ij}=d_{i} \qquad \forall i \in {1,...,n}\] \[\sum_{i=1}^n\textbf{T}_{ij}=d'_{j} \qquad \forall j \in {1,...,n}\]2.3 时间复杂度
上文的线性规划的解法论文中并没有给出描述,因为在计算机视觉学科已经有类似的研究成果了,就是EMD(Earth Mover’s Distance)2,WMD算法也是来源于EMD的思路。
这里我们对具体解法不做详细介绍,只给出几种常见解法的时间复杂度:
更多细节可以参考EMD3和Fast EMD2的论文对时间复杂度的解释。
3. 算法速度改进
由于WMD的时间复杂度较高,论文中给出了两种提升速度方法:WCD和RWMD,为WMD的公式计算一个下界,当做最小值。这种方法在加快了计算速度的同时,也产生了精度损失。
下图是一个实验,对于twitter/amazon的两个数据集,随机抽取一些文本组成句对,将这些句对按WMD分数由小到大排列,横坐标是句对的编号,纵坐标是WMD、WCD和RWMD的值。从图中可以看出,WCD是非常宽松的下界,RWMD非常接近最优解。
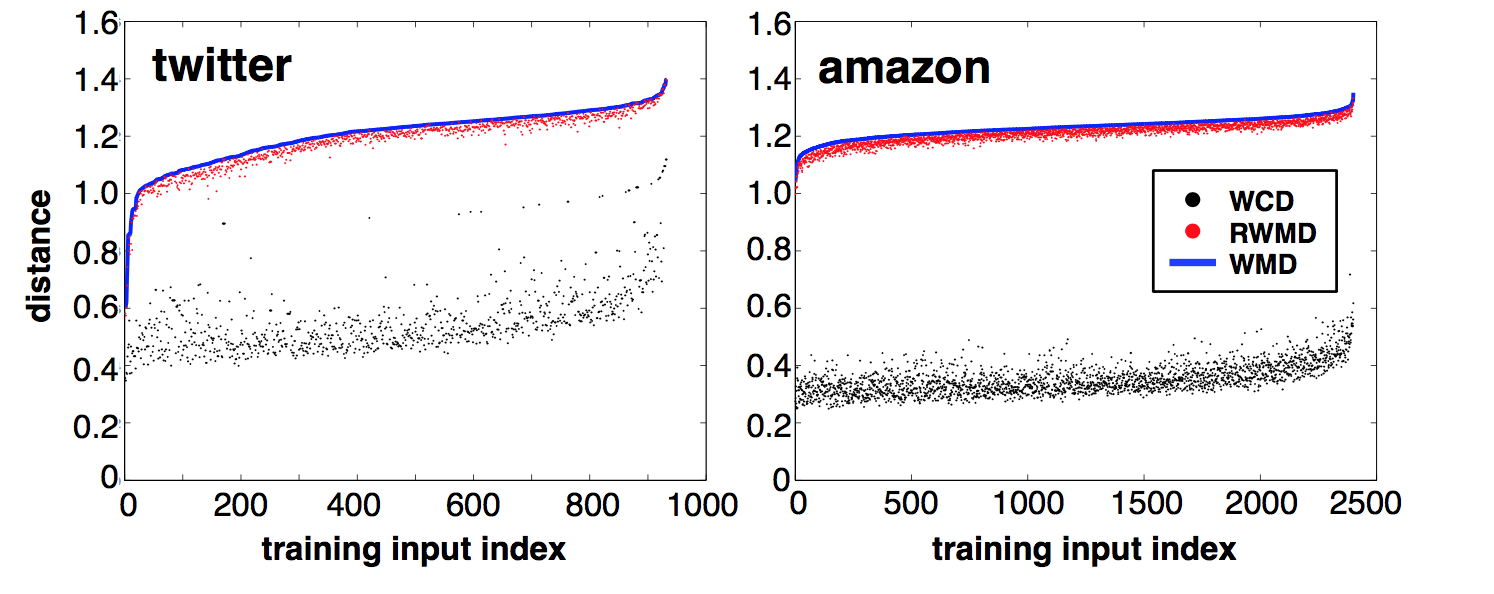
总结:
时间复杂度:WCD < RWMD < WMD
精度:WCD < RWMD < WMD
3.1 WCD
WCD(Word centroid distance)主要利用三角不等式,找到WMD的最优化目标的一个宽松下界,用来替代WMD的结果。其实这种算法的本质上就是我们最快能够想到的计算两条文本相似度的方法:分别把每条文本的词向量加起来取平均,再计算得到的两个向量的欧氏距离。
WCD极大的加快了运行速度,将时间复杂度减小到\(O(dp)\)。其中d代表词向量维度,p代表两篇文本分词去重后词表的大小。
公式推导如下:
现有两条文本\(\textbf{d}\),\(\textbf{d}'\),
3.2 RWMD
尽管WCD很大程度上提升了运行速度,但由于边界过于宽松,效果并不是很好。因此,作者又提出了一种新的优化方法:RWMD(Relaxed word moving distance)。RWMD会计算两次,每次计算时会从WMD两个约束中去掉一个约束,得出两个比WMD宽松的结果,然后取其中的最大值。
如果去掉的是第二个约束,那么最优化目标变成了:
s.t.
\[\sum_{j=1}^n\textbf{T}_{ij}=d_{i} \qquad \forall i \in {1,...,n}\]这个问题的最优解是,对于一条文本中的一个词,找到另一条文本中与之最相近的一个词,全部转移到这个词。即:
\[\textbf{T}^*_{ij}=\begin{equation} \left\{ \begin{array}{**lr**} d_{i} & \text{if $j = \arg\min_{j}c(i, j)$} \\ 0 & \text{otherwise} \\ \end{array} \right. \end{equation}\]去掉WMD的限制条件分别计算两次,会得到两个RWMD的距离\(l_{1}(\textbf{d}, \textbf{d}')\)和\(l_{2}(\textbf{d}, \textbf{d}')\)。两者的最大值是一个更紧的下界:
\[l_{r}(\textbf{d}, \textbf{d}')=\max(l_{1}(\textbf{d}, \textbf{d}'), l_{2}(\textbf{d}, \textbf{d}'))\]这个值比WCD更紧。时间复杂度是\(O(p^2)\)。
3.3 剪枝
对于需要大规模计算文本相似度的任务,我们可以利用WCD和RWMD做启发式的剪枝。如在KNN中使用WMD时,对于每一条测试文本,都需要计算与训练集内每一条文本的距离,这个计算量是非常大的,此时可以利用剪枝的思想进行以下操作:
- 利用WCD计算出所有距离,并按距离从小到大排序,取topk
- 计算topk文本的WMD
- 对于剩下的文本,计算RWMD值。如果RWMD比topk中WMD最大的小,则替换topk中WMD最大的文本;否则,剪枝
在实验中,由于RWMD非常紧,95%的文本都可以被剪枝。
4. 实践
4.1 根据业务场景选择改进算法
在吾来机器人平台中,我们利用WMD算法计算用户query与检索召回的多个相似问的WMD距离,作为排序模型的输入。为了保证精度,我们在计算时并没有采用改进的WCD、RWMD的方法,而是用计算WMD最快的Fast EMD方法得到文本相似度。
是否利用改进的算法取决于业务的要求,由于问答机器人提供的是在线服务,每次只会通过用户query召回数量可控的相似问,因此可以使用WMD。但如果进行分类、聚类方法离线处理大规模数据,优化后的算法节省的时间是可观的。
4.2 工程化
然而,尽管检索召回的的相似问数量可控,Fast EMD达到\(O(p^{3}\log{}p)\)的时间复杂度,WMD计算的速度仍然很慢,在在线服务中产生了难以忍受的性能损耗。 目前开源的WMD实现有:
- gensim(python)调用pyemd的c扩展,使用fast EMD算法。重构之前用的是这个版本,由于是python封装的wmd,计算非常慢。
- 作者Matthew J Kusner实现的wmd( c),使用单纯形法3计算emd。而单纯形法的时间复杂度不稳定,最大为指数级,大多数情况是超立方级,可能会给线上TP99带来毛刺。
- Fast WMD,同样是python封装c。另外,这个项目给出了RWMD的实现。
以上几种开源实现都有各自的缺陷。最后我们没有使用以上几种开源实现,而是用cgo封装Fast EMD,重新实现了WMD算法,产生了惊人的性能提升。
4.3 算法改进
除工程化之外,我们对WMD算法本身也进行了一些改造。在WMD中,向量\(\textbf{d}\)的每一位代表词在文本中的词频,因此在排除出现次数的影响因素的情况下,不同词对于一条文本的贡献是一样的。但实际上在一条文本中,不同词的重要性是不一样的,因此我们用tf-idf替换了词频。
还是利用运输问题类比,在WMD算法中,如果每个词在一条文本中只出现过一次,那么在文本1和文本2的仓库里,每个货物的重量是相同的。
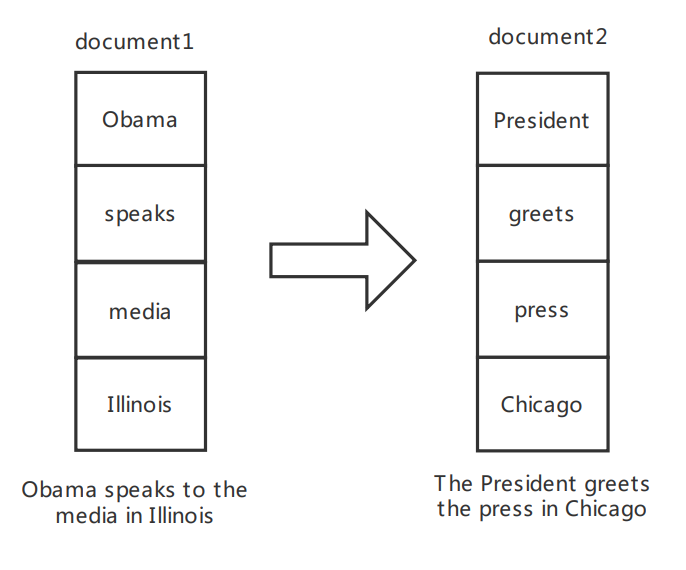
而利用tf-idf替代词频后,货物的重量是不同的,更重要的词将对文本产出更大的贡献
正是WMD的灵活性和健壮性,赋予了我们改造的可能性。
4.4 算法缺陷
WMD有很好的效果,但在处理某些问题时还是存在缺陷:
-
词袋模型,没有保留语序信息:
WMD认为『屡战屡败』和『屡败屡战』在语义上是完全一致的。 -
不能很好的处理词向量的OOV(Out of vocabulary)问题:
由于词向量是离线训练的,应用于在线业务时会遇到OOV问题,用户query分出来的词,有可能找不到对应的词向量。通常,WMD的做法是将新词丢弃。但当OOV的词在文本中起到很重要的作用时,会严重偏离预期。 -
处理否定词能力偏差:
在训练好的词向量中,通常语义相反的词的词向量是比较相近的,这会导致语义相反的两个句子WMD距离很近。
例如,当我们计算『哪些动产能抵押?』和『哪些动产不得抵押?』与『哪些动产不能抵押?』的距离时,我们发现WMD几乎无法分辨否定的语义:
WMD(哪些动产不能抵押?, 哪些动产能抵押?) = 0.1999897183670103
WMD(哪些动产不能抵押?, 哪些动产不得抵押?) = 0.21288069203066828 -
处理领域同义词互斥词的能力偏差:
在不同领域和上下文中一个词可能有不同的含义。
比如在医疗领域『鸡胸』是一种胸骨的畸形的疾病,在烹饪领域『鸡胸』是一种食材。利用通用词向量无法很好的处理这种情况。但如果我们利用领域数据训练词向量,由于语料较少,OOV会比较严重。在WMD中,这两个问题会互相打架。
在不同的上下文中,一个词也有可能有很多不同的含义:他说:“她这个人真有意思(funny)。”
她说:“他这个人怪有意思(funny)的。”
于是人们认为他们有了意思(wish),并让他向她意思意思(express)。
他火了:“我根本没有那个意思(thought)!”
她也生气了:“你们这么说是什么意思(intention)?”
事后有人说:“真有意思(funny)。”
也有人说:“真没意思(nosense)”。
尽管WMD不能解决所有问题,但我们将WMD距离作为一个特征输入到排序模型中,排序模型会融合多种不同的特征,最终给出一个更精确的回复。